[10000印刷√] 円錐 の 表面�� の 求め 方 公式 717386-円�� 高さ 求め方 三平方以外
角錐・円錐の表面積 立体すべての面の面積の合計のことを 表面積 と言います。 例えば次の三角錐の表面積を考えてみましょう。 表面積を求めよという場合は、右図のように展開をして、4つの面の面積を1つずつ求めてそれらを足すことで、角錐の表面積 円錐の表面積や体積を求める公式の覚え方で、語呂合わせ 円錐の表面積や体積を求める公式の覚え方で、語呂合わせ教えてください! 表面積は展開図を描けば、簡単に求められるので 暗記するまでもありません 展開図を描いてわからなければ 扇形も上の円の面積を同じ求め方ができます。 扇形の面積=円弧÷2×半径 円錐の表面積(まとめ) 底面 底面の面積=半径×半径×314 側面 側面の扇形の円弧の長さは底面の円周の長さと同じなります。 です。 「扇形の面積=円弧÷2×半径」なので となり

中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン By 東京個別指導学院
円錐 高さ 求め方 三平方以外
円錐 高さ 求め方 三平方以外- 一般的に、錐の体積公式は以下のように表されます。 錐の体積 底面積×高さ×1/3 そして、これを円錐についてより具体化すると、 円錐の体積の求め方 半径×半径×3.14×高さ×1/3 (πr²×h×1/3) となります。 円錐の場合、底面は円の形となる まずは公式にしたがって円錐の底面積を求めましょう。 底面積 $$\pi \times 3^2=9\pi(cm^2)$$ 次は母線と半径をかけて、側面積を求めます。 側面積 $$8\times 3\times \pi=24\pi(cm^2)$$ 底面積と側面積がそれぞれ求まれば、あとは合計すれば終わり。 表面積




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
展開図を描く段階では、おうぎ形の中心角が分からない状態なので、概形(だいたいの図)で問題ない。 さて円錐の表面積の求め方は少々長いが、理解していただけただろうか。 手順としては ということを行っている。 このうち3については 前章・弧円錐 (えんすい)の表面積の求め方は (底面の半径×底面の半径×円周率) (底面の半径×母線×円周率)です。 展開図にして見るとわかりやすいと思います (3)の図形は底面の半径が3、母線が5、高さが4の円錐です 1 ♡みみ♡ 約2年前A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 弓形 A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐
円錐の展開図は上図のようになります。 まずポイントとなるのは扇の∠BACの大きさです。 半径r の円の円周と円弧BCの長さが一致するので となります。つまり, であるので,扇部分ABCの面積をFとすると となります。 また残る半径r の円の面積は なので円錐台の体積 大変助かりました。 エンジンのシリンダーヘッドのスキッシュエリアの体積を求めるのに使わせて頂きました。 こども園の園庭に作るつきやま盛土の体積を求めるために役立ちました。 バケツの中に降り積もった雪の体積を測定したくて 公式の覚え方 中学校では次のような公式を習うかと思います。 円の半径を r r 、同じく球の半径を r r とすると、 円の面積は A= \pi r^2 A = πr2 円周は \ell = 2\pi r ℓ = 2πr 球の体積は V=\frac {4} {3} \pi r^3 V = 34πr3 球の表面積は S= 4\pi r^2 S = 4πr2 この式を見比べ
円錐の表面積 立体の表面積は各面の面積を求めて,その和を出す。 円錐は底面が円で,側面はおうぎ形である。 側面のおうぎ形の弧の長さは底面の円周の長さに等しい。 底面の半径3cm, 母線の長さ10cmの円錐の表面積を求めよ。 中1 円錐の表面積 10cm 3cm今日は円錐の表面積について学習していくよ。 下の図の円錐の表面積の求め方について考えていきましょう。 生徒 円錐は展開すると下の図のようになります。 すると底面の円と側面のおうぎ形の面積の和が表面積になります。 ただ底面の円の面積はπ1分でわかる公式、問題と高さの求め方、証明 円錐の側面積は?1分でわかる求め方、公式、母線と半径の関係、例題 100円から読める!ネット不要!印刷しても読みやすいpdf記事はこちら⇒ いつでもどこでも読める!広告無し!建築学生が学ぶ構造力学のpdf
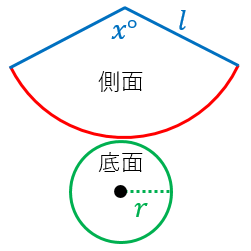



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su
上の円錐の表面積は、暗算でできるんです。 底面積は3×3×π=9π 側面積は3×5×π=15π足して24πです。 たったこれだけで終わりです。 中学校では教えてくれないやり方です。 これはどんな円錐でも当てはまります。 ちなみに公式は底面の半径をa、母線 《円錐の体積の求め方》 円錐の体積=底面積×高さ÷3なので 答え 096cm³ スポンサードリンク 問題③ 体積が1570cm³である次の円錐の高さを求めましょう。 (円周率は314とします。) 《円錐の高さの求め方》 円錐の体積=底面積×円錐の高さ÷3であること 円錐の側面積の簡単な出し方を使って、円錐の表面積の出し方の公式を導き出す こともできます。 円錐の側面積に円錐の底面積をあわせれば、円錐の表面積ですので、 円錐の側面積+円錐の底面積 円周率(π)×母線×底面の半径 + 円周率(π)×底面




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
円錐の表面積は円錐の底面積 (下の部分)と側面積 (横の部分)を分けて考えます。 円錐の底面積の半径をr、母線をmとすると、 (底面積)=r×r×π=πr^2 (側面積)=1/2Lm (←扇型の面積の公式,L=扇型の弧の長さ) =1/2×2πr×m=mrπ よって、円錐の表面積はπr^2mrπになり 扇形の面積を求める公式を導出する 円錐の側面積 = LRπ で求めることができることがわかりましたが、この式を変形してみます。 式を変形 小文字になってしまっていますが気にしないでください。 理由はありあません。 私のミスです。 ここで、2 r π これは大事な公式ですからしっかりと覚えておきましょう。 円の面積の求め方は、 (円の面積) = (半径) × (半径) × (円周率π) ですね。 ここまでわかれば、準備完了です。 ・底面の円の面積は 3×3×π=9π㎡ ・高さは 8cm よって、求める円柱の




回転体 円錐の体積と表面積の求め方 現役塾講師のわかりやすい中学数学の解き方




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる
角錐と円錐の体積 角錐と円錐の体積も同じ公式です。 底面積を S 、高さを h とすると、体積 V は以下の公式になります。 V = 1 3 S h 公式に 1 3 が付いている理由は、高校数学で積分を習うとわかります。 難しい計算なので、今は無理矢理 1 3 が付くと納得 円すい展開図・表面積の公式 の求め方 一つの式で書く $底円の円周の長さ=r\times2\times314$ $半径Rの円周の長さ=R\times2\times314$ おうぎ形の弧の長さは、底円の円周の長さと同じ長さなので、 $おうぎ形の弧の長さ =r\times2\times314$ おうぎ形と半径Rの円を比べると いよいよ問題のとんがってる部分の面積だね ここは展開して考えるよ 展開するとこうだね だから、扇の面積を求めるためには中心角を求める必要があるよ。中心角の求め方を忘れてしまった人は、扇形の中心角の求め方3パターンピザでわかるを見てね




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



円錐とは 体積 表面積の公式や求め方をわかりやすく解説 受験辞典
上記のように、円錐の側面積の公式が導出できました。扇形の面積の求め方は下記が参考になります。 扇形の面積は?1分でわかる意味、公式、求め方、ラジアンとの関係 円錐の側面積を求める例題 例題として、下図に示す円錐の側面積を求めましょう。 ※円周率πは無理数ですので、小数点以下の最後の数は参考値とされてください。 円錐の公式(計算式) 体積V表面積S側面積F半径r母線R 体積V V = 1 3 π r 2 h 表面積S S = π r r R 側面積F F = π R r 円錐の側面積の公式 まずは、公式だけ図でさっと確認するよ つぎに、円錐の特徴を確認して、そのあとに側面積を求めていくよ 円錐の特徴 円錐の特徴は主に次の二つだよ




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト
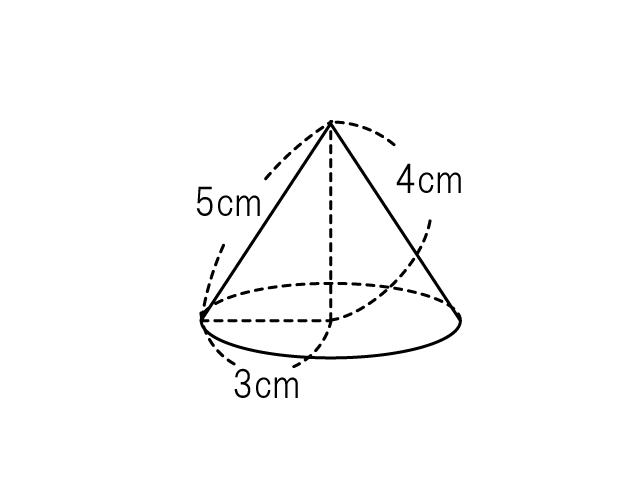



円すい 円錐 の体積の求め方と問題 小学数学 Irohabook
円錐の体積の求め方 公式と計算例 Scipursuit 体積の求め方 円錐 円錐の体積を求める公式は、次の通りです。 V = 1 3Sh = 1 3πr2h V = 1 3 S h = 1 3 π r 2 h ここで、V は円錐の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の




空間図形14 円すい台の体積 Youtube




裏ワザ公式 円すいの側面積を一瞬で求める方法 Youtube




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



円錐の側面積は 1分でわかる求め方 公式 母線と半径の関係 例題




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題



3




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン By 東京個別指導学院




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




角錐 円錐の体積と表面積の公式 数学fun




円錐の表面積の求め方 公式と計算例




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学



円錐とは 体積 表面積の公式や求め方をわかりやすく解説 受験辞典
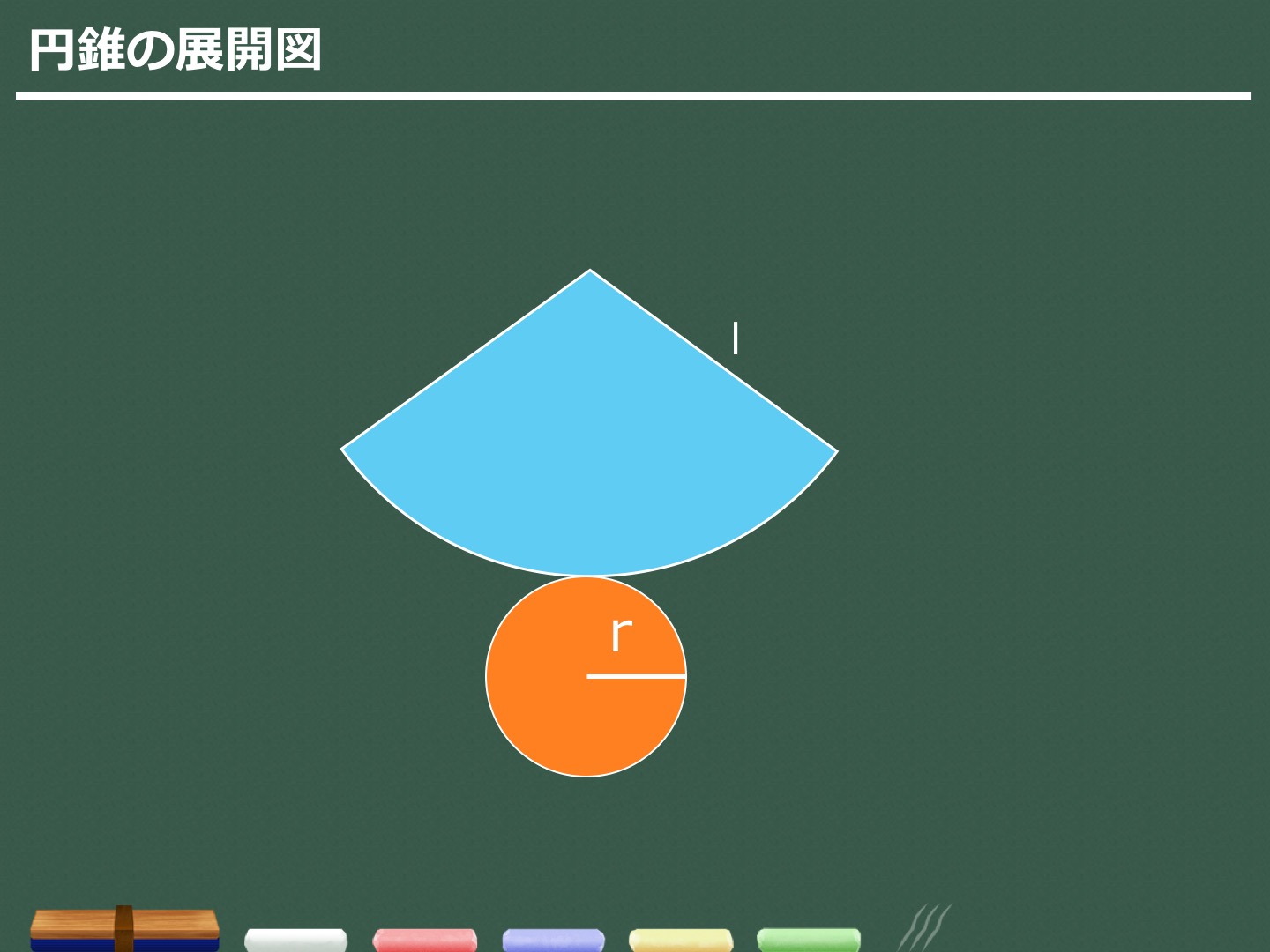



3分で分かる 円錐の体積 表面積の求め方をわかりやすく 合格サプリ



Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ



円錐とは 体積 表面積の公式や求め方をわかりやすく解説 受験辞典



円錐とは 体積 表面積の公式や求め方をわかりやすく解説 受験辞典




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円すいの展開図 表面積の求め方 公式があるの知っていますか




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



できる 中学の数学 円錐の表面積 の出し方 3つの方法 で不安解消




円錐の表面積の求め方 公式と計算例
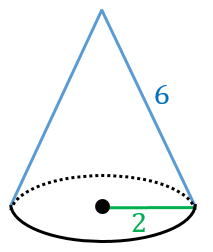



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




円錐の側面積 展開図の扇形の中心角 教科書から 身勝手な主張
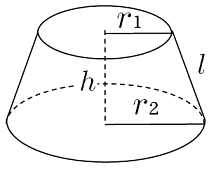



初等幾何 円錐台の側面積を求める 大人が学び直す数学




表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題




角錐 円錐の体積と表面積の公式 数学fun
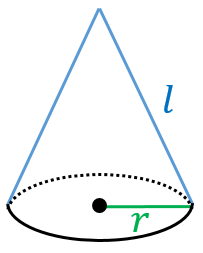



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




3分で分かる 円錐の体積 表面積の求め方をわかりやすく 合格サプリ




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



1




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




中学数学 回転体の体積 表面積を求める問題を解説するぞ 中学数学 理科の学習まとめサイト
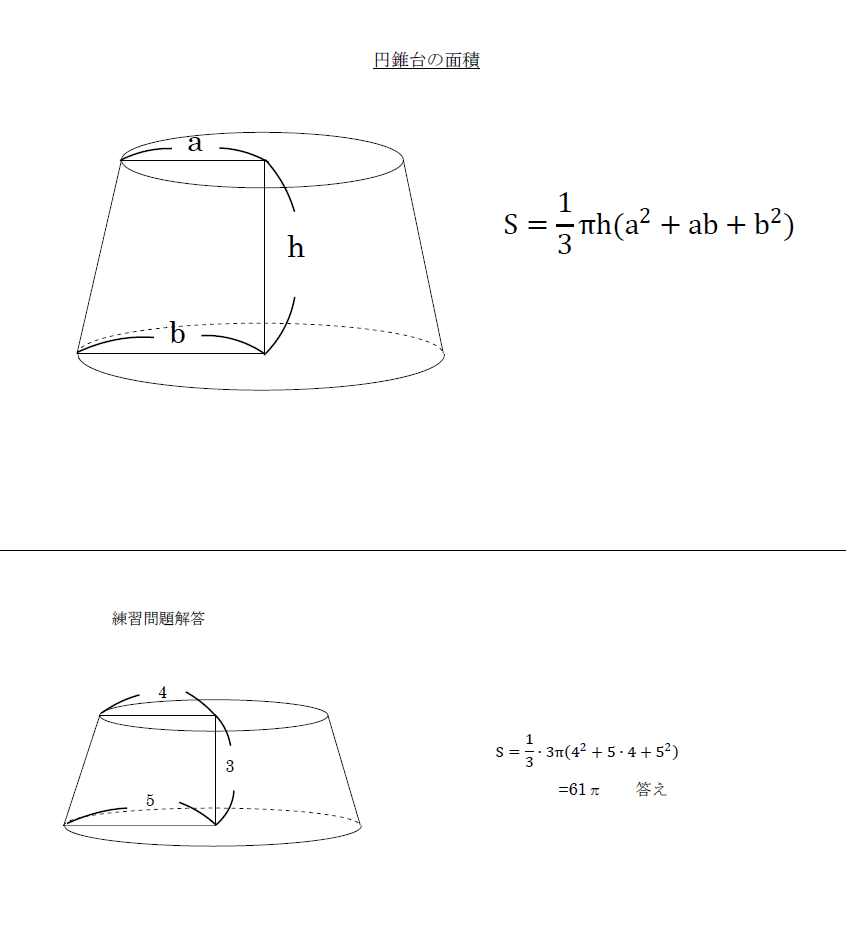



受験 定期試験 数学解き方集 裏技 解法 空間図形の体積 円錐台 の解法 中学




円錐の体積ってなんであの公式なの Webty Staff Blog




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室




中3 三角形の相似 円錐の体積比 日本語版 Youtube




瞬殺 円錐の表面積を3秒で求める裏技 中学数学 空間図形 3 Youtube




円錐の体積ってなんであの公式なの Webty Staff Blog
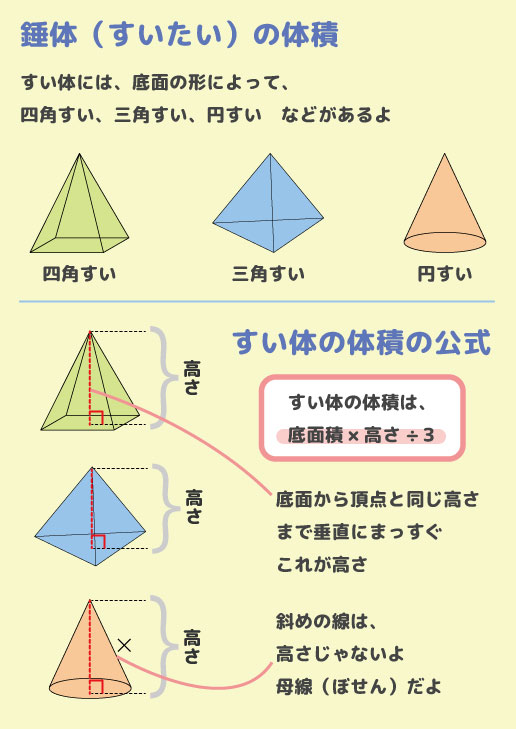



中1数学 すい体の体積と円すいの表面積 数学検定5級 お家でお勉強




表面積の求め方 計算公式一覧




高校入試対策数学 円錐に関する対策問題 Pikuu




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



3




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ
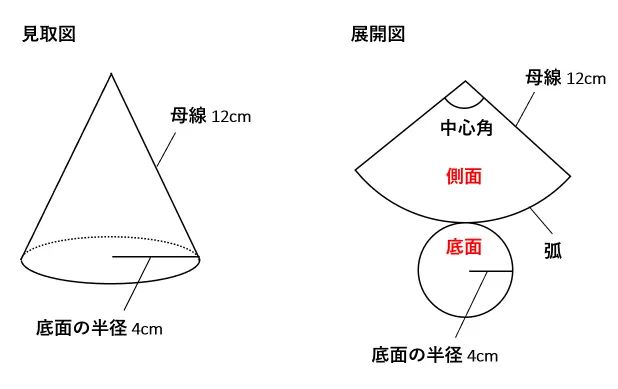



円錐の表面積を公式で求めよう 母線と底面の半径だけで簡単に計算できる 中学受験ナビ



円錐とは 体積 表面積の公式や求め方をわかりやすく解説 受験辞典
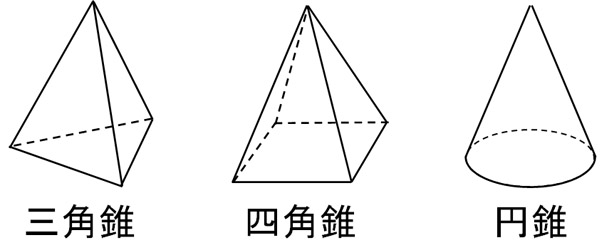



角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 Hatsudy 数学 科学




円錐の表面積 あんず学習塾のメモ 図表置き場
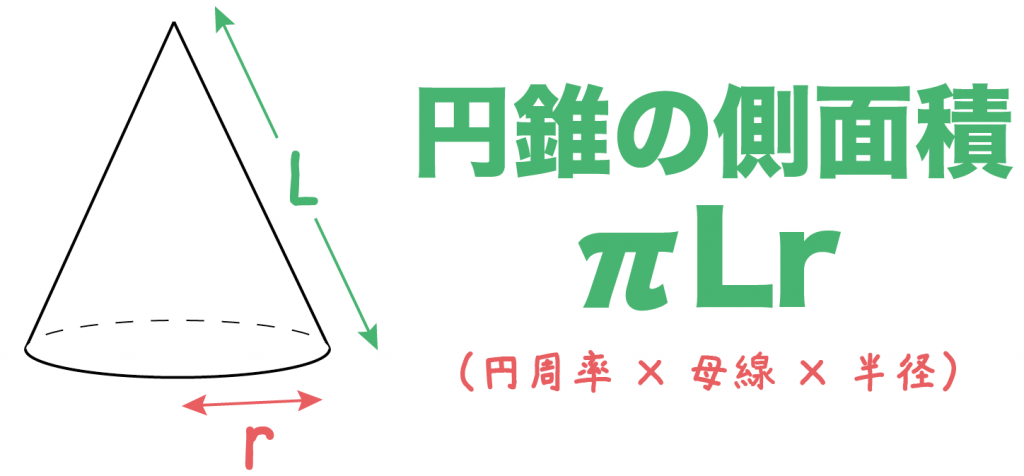



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の表面積 Youtube



File Bicone Svg Wikipedia




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学
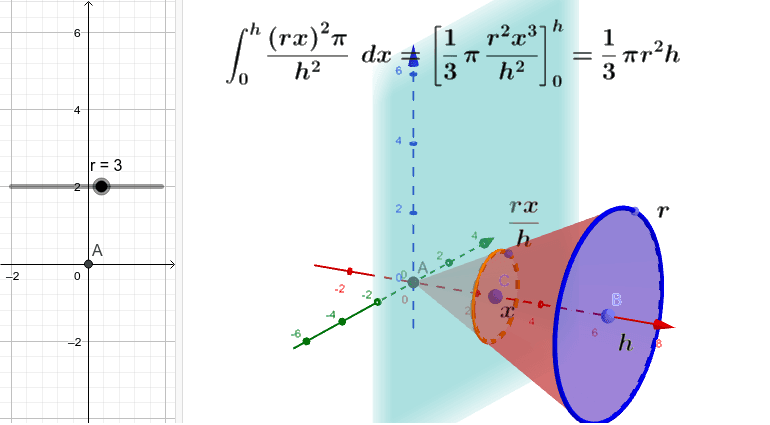



円錐の体積の求め方 Geogebra




球の表面積と体積の公式 数学fun




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ



Studydoctor円錐や角錐の体積の求め方 中学1年数学 Studydoctor




円錐の表面積を 公式を使って求める チーム エン
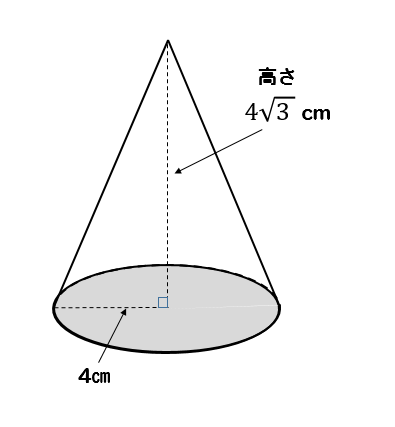



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ



円錐の表面積の求め方で赤い線の部分と底面の半径とpをかけたら Yahoo 知恵袋



図のような円錐台の体積を求めるにはどのような計算をすればよいか教えてください Yahoo 知恵袋




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積を公式で求めよう 母線と底面の半径だけで簡単に計算できる 中学受験ナビ




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
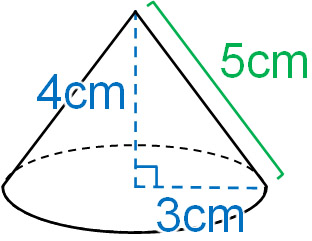



角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 Hatsudy 数学 科学



球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




角錐 円錐の体積と表面積の公式 数学fun




Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ




角錐 円錐の体積と表面積の公式 数学fun




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順




円錐の体積の求め方 公式と計算例




3分で分かる 円錐の体積 表面積の求め方をわかりやすく 合格サプリ



写真の円錐の体積と表面積を求める問題なんですが この答えであっているでしょ Yahoo 知恵袋
コメント
コメントを投稿